Research

Back to my homepage

Contributions

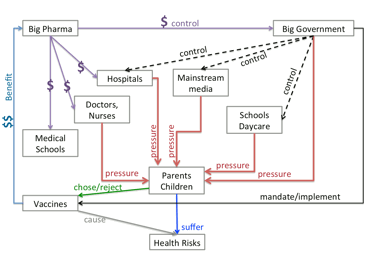
Learning a Content from Unstructured Corpus of Text Data! Chasing Exemptions: Social Media, Big Data, and the Measles Crisis E. Ebrahimzadeh- M. Falahi- T. Tangherlini- V. Roychowdhury- A. Wadia The 2014-2015 measles outbreak in California caught many observers by surprise. Health officials attributed the crisis to the increasing number of children whose parents had secured exemptions from inoculation for various vaccine-preventable diseases (VPDs), without providing a quantifiable analysis of what was driving these exemptions. Focusing on two social media sites popular among mothers, we show that large-scale text analysis tools can be used both to identify vaccine-related conversations and to discover the topic of these conversations. We uncover a strong, persistent signal focusing on securing exemptions for childhood vaccinations. We consider this type of signal to indicate that the conversations about exemptions are “endemic” to these sites. If people take real-world actions based on the suggestions in these conversations, the cumulative effect would contribute to a diminution of herd immunity in their communities. This effect has been borne out by real world events. Our method based on analyzing social media chatter at scale can provide an alert mechanism to health officials and to others charged with early childhood health decisions, helping to discover “hidden” health crises such as the current one surrounding childhood vaccination. Journal Version: Submitted to Proceedings of the National Academy of Sciences

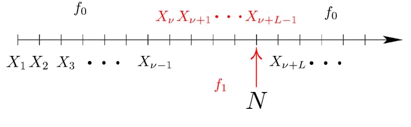
Finding a Needle in Haystack Efficiently! Quickest Transient Change Point Detection with Sampling Constraint E. Ebrahimzadeh- A. Tchamkerten Consider the problem of sequential detection of a transient change in distribution of a random sequence, where there is a constraint on the fraction of samples observed. We cast the problem into a Minimax setting, where the change time is completely unknown, all random variables are independent and both the distributions along the change and pre/post change are known. The objective is to design a statistical test with large average time to false alarm to minimize a measure of worst case delay. Leveraging the results in the non-transient setting, we show that there exists an asymptotic threshold on the minimum duration of a change that can be detected reliably with such false alarm constrained statistical tests. Next, given a transient change with duration above this asymptotic threshold, we characterize the smallest sampling rate needed so that under sparse sampling the change can be detected as efficiently as under full sampling. Conference Version: proceedings of ISIT 2015

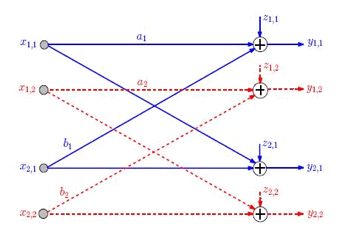
Let Signals Mix up! Signalling in Frequency-Selective Interference Channels: Outage Analysis E. Ebrahimzadeh- K. Moshksar- A. Khandani We study outage probability in a two-user parallel Gaussian interference channel consisting of two parallel sub-channels. Each sub-channel is modeled by a two-user Gaussian interference channel with quasi-static and flat fading. Each user employs a single-layer Gaussian codebook, splits its average transmission power equally and maintains a statistical correlation between the signals transmitted over the underlying sub-channels. Under mild non-degeneracy conditions on the fading statistics, it is shown that the value of correlation coefficient that minimizes the outage probability approaches 1 as the signal-to-noise ratio (SNR) approaches infinity. This holds whether the receivers treat interference as Gaussian noise (TIN) or cancel interference (CI). We compute the outage probability for sufficiently large SNR under the assumptions that the correlation coefficient is 1 and the direct and crossover channel coefficients are independent zero-mean complex Gaussian random variables with possibly different variances. In particular, it is shown that if the receivers have the freedom of choice to perform TIN or CI, a smaller outage probability is achieved in contrast to a scenario where the users are orthogonal, i.e., interference is completely avoided by assigning disjoint sub-channels to the users. Journal version: Revised for IEEE Transactions on Information Theory Conference Version: Proceedings of ISIT 2015
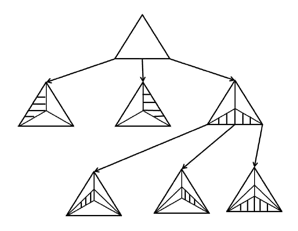
It’s a Small world in Random Apollonian Networks! On the Longest Path and Diameter of Random Apollonian Networks E. Ebrahimzadeh- L. Farczadi- P. Gao- A. Mehrabian- C. Sato - N. Wormald- J. Zung We consider the following iterative construction of a random planar triangulation. Start with a triangle embedded in the plane. In each step, choose a bounded face uniformly at random, add a vertex inside that face and join it to the vertices of the face. After n − 3 steps, we obtain a random triangulated plane graph with n vertices, which is called a Random Apollonian Network (RAN). We show that asymptotically almost surely (a.a.s.) every path in a RAN has length o(n), refuting a conjecture of Frieze and Tsourakakis. We also prove that a.a.s. the diameter of a RAN is asymptotic to c log n, where is the solution of an explicit equation. Journal version: In Random Structures and Algorithms(RSA)-December 2014 Short version published in Electronic Notes in Discrete Mathematics
There is Room for Opportunism in Random Access! Random Access in Wireless X-Networks S. Mahboubi-E. Ebrahimzadeh-A. Khandani We studied a 2-user symmetric X channel with random access capability for transmitters. Transmitters can work in two modes of operation independent of each other, either active or inactive. There is an independent message from each transmitter to each receiver. It is aimed in this study at maximizing the throughput of this network over the set of rates which can be reliably communicated. To characterize this rate region, an information theoretic outrebound is derived. Achievability is based on opportunistic signal transmission along with a linear pre-coding scheme. Once the rate region is exactly determined, throughput maximization can be solved as a linear programming problem. In this work, we followed the footsteps of Minero et al. for modeling random access in an information theoretic framework, The coding scheme we used for tackling this problem is based on the new deterministic model proposed by Niesen and Maddah-Ali, where capacity region of the X-channel is approximated within constant bit. Conference version: Proceedings of ISIT 2012
It’s Better to Look at Things from both Sides! Sufficient Conditions for the Existence of Fix-free codes E. Ebrahimzadeh-M. Khosravifard-A. Aghajan-A. Gulliver A code is said to be fix-free if any code-word is neither a prefix nor a suffix of any other. Using fix-free codes, the decoding speed can be doubled and the robustness to transmission errors is increased. It is conjectured by Ahlswede et al. in [1] that there exists a fix-free code for a length vector, if the Kraft sum of a length vector is less than 3/4. We showed that this conjecture is true for all length vectors of size less than or equal to 32 and improved the known upper bounds for a certain class of length vectors. This problem is tackled as a counting problem using the principle of inclusion-exclusion combining with a novel idea introduced by Yekhanin to prove the existence of a fix-free code for length vectors with Kraft-sum less than 5/8. Journal version: Accepted for publication in IEICE Trans. on fundamentals of Communications Weakly Symmetric Fix-free codes A.Aghajan- M. Khosravifar (I have collaborated in this work) A fix-free code is said to be symmetric if each code-word is a palindrome. These codes provide more error resilience and are proved to be more suitable for joint source-channel coding than the asymmetric ones. Moreover, the same codebook can be used for the forward and backward decoding. Maintaining these advantages, we defined a new class of fix-free codes, so called Quasi-symmetric fix-free codes, with certain symmetry properties and provided sufficient conditions for the existence of these codes. In fact, we imposed the symmetric condition over the whole codebook rather than each single code-word. This means that if a code-word is not a palindrome, then the reverse code-word should be in the code-book. We first showed that the set of Quasi-symmetric fix-free codes is a strict subset of Asymmetric fix-free codes, then provided evidence that the ¾ conjecture still holds for this class of fix-free codes. In particular, we showed that the 5/8 upper-bound is also a sufficient condition for Quasi-symmetric codes.

Journal version: Published in IEEE Transactions on Information Theory